Содержание к диссертации
Введение
Глава 1. Основные понятия и описание существующих методов определения ЧОТ 14
1.1 Основные понятия в цифровой обработке сигналов 14
1.1.1 Импульсно-кодовая модуляция 14
1.1.2 Дискретное преобразование Фурье 14
1.1.3 Быстрое преобразование Фурье 16
1.1.4 Оконные преобразования 16
1.2 Алгоритмы оценивания ЧОТ 17
1.2.1 Классические алгоритмы во временной области 18
1.2.2 Классические алгоритмы в частотной области 22
1.2.3 Алгоритм YAAPT 28
1.2.4 Алгоритм MBSC 29
1.2.5 Алгоритм SWIPE 30
1.2.6 Алгоритм WU 30
1.2.7 Алгоритм YIN 31
1.2.8 Алгоритм PEFAC 32
1.2.9 Алгоритм High accuracy and octave immune pitch detection 32
1.2.10 Алгоритм Pitch estimation using models of voiced speech on three levels 33
1.2.11 Алгоритм IRAPT 33
Глава 2. Определение параметров модели голосового сигнала 35
2.1 Оценивание комплексных амплитуд голосового сигнала по МНК 35
2.1.1 Аффинные колокольчики 38
2.1.2 Вычисление коэффициентов квадратичных форм 42
2.1.3 Нормализованные колокольчики 46
2.1.4 Решение предельных уравнений МНК 48
2.2 Несмещённый критерий оценки периода основного тона 52
2.2.1 Модель измерения с белым шумом з
2.2.2 Расчёт подавляемой части шума 55
2.2.3 Критерий оценки периода основного тона по эмпирической дисперсии
2.2.4 Стационарная аппроксимация 62
2.3 Ввічисление показателей качества для целвгх значений периода 65
2.3.1 Аффинная моделв с целвім периодом основного тона 66
2.3.2 Стационарная моделв с целвім периодом основного тона 69
2.3.3 Болвшой целвш период 72
2.4 Локалвнвіе ввічислителвнвіе алгоритмві 79
2.4.1 Решение системві линейнвіх уравнений 79
2.4.2 Локалвная подстройка оценки ЧОТ 81
Глава 3. Алгоритм быстрого оценивания ЧОТ 87
3.1 Постановка задачи 87
3.1.1 Минимизируемая функция 87
3.1.2 Частнвш случай 89
3.2 Свойства функции «колоколвчик» 89
3.2.1 Расчёт пределвного колоколвчика 90
3.2.2 Точноств пределвного колоколвчика 91
3.2.3 Полиномиалвная аппроксимация 96
3.3 Аппроксимация функции ф{Р) 99
3.3.1 Факторизация знаменателя 100
3.3.2 Аппроксимация ф0(Р) при помощи сглаживающей функции 103
3.3.3 Аппроксимация функции ф0(Р) при помощи ряда Лорана 109
Глава 4. Экспериментальные результаты 118
4.1 Демонстрация работві алгоритма определения ЧОТ 118
4.2 Сравнение с существующими алгоритмами определения ЧОТ 122
Заключение 123
Список литературы
- Импульсно-кодовая модуляция
- Вычисление коэффициентов квадратичных форм
- Частнвш случай
- Сравнение с существующими алгоритмами определения ЧОТ
Импульсно-кодовая модуляция
Несмотря на свою вычислительную сложность, методы определения ЧОТ на основе ДПФ являются широко используемыми, даже в задачах реального времени. Переход в частотную область позволяет увидеть те свойства сигнала, которые в условиях временной области увидеть практически невозможно.
К примеру, синусоидальный сигнал, передаваемый по проводам, может накопить в себе достаточно сильные шумовые помехи. Взглянув на такой зашумлённый сигнал в нём можно даже не заметить периодической составляющей. Но после применения ДПФ сразу станет ясно, что в сигнале присутствует гармоническая составляющая. К примеру, на рис. 1.5 приведён график сигнала, аддитивно составленного из гармоник с частотами 90 и 150 Гц, а так 300
Спектр голосового сигнала. же шума. Визуально выделить гармоники не представляется возможным. На рис.1.6 представлен спектр того же сигнала. На спектре легко заметить характерные пики в областях частот гармоник, присутствующих в сигнале. Этот пример показывает потенциал методов, основанных на анализе сигнала в частотной области.
Метод на основе детектирования пиков спектра Этот метод нацелен на поиск пиков спектра, равноудалённых друг от друга. Основы-ваясь на физике процесса синтеза голосового сигнала человеком, в спектре должны присут-ствовать гармоники, частота которых кратна ЧОТ. На рис. 1.7 приведён пример спектра голосового сигнала.
Можно проводить дополнительные действия для увеличения качества работы такого класса алгоритмов. В работе [48] использовался метод аппроксимации пиков спектра параболами. Из всего набора пиков выбирался максимальный по амплитуде. Он считался частотой одной из формант. Далее выяснялся номер этой форманты путём поиска на спектре соседних пиков, определённым образом удалённых от текущей форманты.
В работе [49] были использованы нейронные сети для уточнения частоты пика на спектре сигнала. В качестве входа нейронной сети использовались три точки на спектре, представляющие интересующий пик.
Спектральная корреляция Метод спектральной корреляции детектирует ЧОТ путём сравнения сигнала с идеаль-ной моделью. Подразумевается, что входной сигнал является голосовым и состоит лишь из гармоник, кратных ЧОТ [50]. Синтетический сигнал создаётся для некоторого набора кандидатов на ЧОТ. Та модель, чей спектр больше всего совпадает со спектром исходного сигнала, выбирается как верная. Процесс подобен автокорреляционному методу во временной области.
Lahat [51] предложил использовать корреляционный метод в частотной области. Спектр пропускается через 16 фильтров, которые покрывают диапазон поиска ЧОТ. Для каждого выхода фильтра вычисляется автокорреляционная функция. После этого принимается общее решение для значения ЧОТ. Harmonic Product Spectrum Метод HPS был рассмотрен в работах [52-54]. Алгоритм оценивает ЧОТ как частоту которая максимизирует произведение амплитуд спектра, взятых в кратных этой частоте отсчётах: п /o = argmaxTT№/)l, (1.3) fc=i где X -- спектр сигнала, п — количество рассматриваемых гармоник, и /о — оценка ЧОТ. Ограничение на количество гармоник п имеет смысл для ускорения вычислений, но не несёт какого-либо иного смысла. Если в формуле (1.3) взять логарифм от произведения, то его можно внести под знак произведения и формула примет аддитивный вид: п /0 = argmaxVlogX(fc/). (1.4) fc=i Это вторая форма описания алгоритма HPS. У такого подхода есть несколько слабых мест. Этот метод плохо работает с короткими сигналами, длина которых не превосходит трёх периодов. Так же алгоритм будет плохо работать, если хотя бы одна из формант будет от-сутстовать на спектре по каким-либо причинам (зашумлённость, искажения канала и т.п.).
В работе [55] предложен похожий алгоритм, в котором вместо произведения используется напрямую сложение частот:
Эта формулировка позволяет избежать проблем с отсутствующими формантами. Но тут возникает другая проблема: предположим, у нас имеется сигнал с единственной гармоникой в / Гц. Тогда, любая из гармоник f/n будет иметь тот же вес, что и /, т.е. с той же уверенностью может являться ЧОТ, что неверно. Такую проблему можно решить, введя весовые коэффициенты: где г = 0.84 — эмпирически подобранное значение.
В статье [56] предложена ещё одна модификация такого рода подхода. В ней используются не только пики спектров, но и их некоторая окрестность:
В условиях голосового сигнала основную идею можно описать следующим образом: спектр должен иметь набор пиков, равноудалённых друг от друга на значение ЧОТ. Следовательно, если сигнал сжать в і число раз, то г-ая форманта совпадёт с ЧОТ. Метод включает в себя 3 шага: вычисление спектра сигнала, его сжатие и произведение с исходным спектром. Рассчитывается спектр S\. Затем происходит его сжатие в 2 раза и в результате имеем 5 2. Пик второй форманты в S2 должен совпасть с пиком ЧОТ, и так далее. На рис. 1.8 приведёна схема работы алгоритма. Видно, что гармоники накладываются в районе 170 Гц.
Вычисление коэффициентов квадратичных форм
Утверждение 2 теоремы 1 показывает, что в практических расчётах можно заменять коэффициенты уравнений МНК на их предельные значения. Погрешность в целом обратно пропорциональна N2, где N - количество отсчётов во фрейме. Погрешность элементов тёп-лицевой матрицы убывает обратно пропорционально кубу номера диагонали, что говорит о слабом влиянии этой погрешности на число обусловленности обращаемой матрицы.
В дальнейшем зависящие от N матрицы уравнений МНК будут часто заменяться своими предельными значениями, что упрощает формулы и графики и как правило не влияет на качественный результат. Векторы Аоо, В , составляющие решение предельного уравнения МНК будем называть предельными комплексными оптимальными амплитудами. Величину min,co назовём предельным минимальным значением функционалом качества.
После нормализации матриц и множителей предельное уравнение уравнение МНК описывается следующим утверждением. Следствие 1. Векторы предельных комплексных оптимальных амплитуд А = А,со)1_м и Boo = (Bk,oo)f=-M определяются из условий в = соЦтр оо Дх,), где в -решение уравнения что по определению совпадает с уравнением рв = у при 0 = 7_1гоо и У = 7 оо. С Основное уравнение МНК после нормализации рв = у имеет следующую особенность: на главной диагонали матрицы р стоят 1, а все остальные элементы меньше по абсолютной величине. В ряде алгоритмов эта особенность упрощает численную реализацию решения и изучение его свойств.
Естественным критерием качества модели речевого сигнала %{Р,А,В), зависящей от периода Р и векторов амплитуд А, В, выглядит среднеквадратичная погрешность N/2-1 Е(Р,А,В)= J2 \wt(st-st(P,AB))\2. n=-N/2 Минимизацию этой функции можно провести последовательно: min Е(Р, А, В) = min [min Е(Р, А, В)} = min [min JP(A, В)} . Р,А,В Р А,В Р А,В где Jp(A,B) — функционал, минимизация которого изучалась в предыдущем разделе, при фиксированном значении периода основного тона Р и, соответственно, частоты F = N/P.
Однако точка минимума функционала Е(Р,А,В) в действительности плохо подходит для оценки параметров данной модели. В частности, множество моделей с фиксированным значением Р и произвольными А, В содержится в классе аналогичных моделей с удвоен-ным периодом 2Р. Отсюда минимум Е будет всегда достигаться на удвоенном периоде, что нежелательно. Эффективный подход к определению периода основного тона был предложен в известной статье [12]. Идея состоит в оценке дисперсии белого шума, входящего в модель сигнала. Результат оценивания традиционно называется несмещённым критерием оценки периода основного тона.
Статья [12] написана без строгих доказательств, в ней интегралы многократно заменяются конечными суммами и наоборот, а спектры соседних гармоник считаются непересекающимися. Тем не менее, правильная реализация предложенной идеи эффективна, так как минимизация эмпирической дисперсии белого шума приводит к оценке, часто совпадающей с оценкой максимума правдоподобия.
В данном разделе будет точно рассчитана величина эмпирической дисперсии белого шума и тем самым, построена оценка периода основного тона, близкая к максимуму правдоподобия. Как и в несмещённой оценке из [12], эта дисперсия отличается лишь множителем от минимума квадратичного функционала качества Jmm. Этот множитель зависит от количества F периодов на анализируемом фрейме и совпадает с множителем из [12], начиная примерно с F 3.5. На коротких фреймах, содержащих менее трёх или даже двух периодов, множитель существенно меняется.
Наряду со стационарной моделью, изучавшейся в [12], рассмотрена также аффинная модель, для которой получены аналогичные результаты. Пусть измеряемая величина St отличается от идеальной модели только шумовой составляющей: V ake Fkt + bk—еЛ +v -N/2 t N/2-1, где a = (ак)к=_м и b = {Ьк)к=-м ”истинные” комплексные амплитуды гармоник, а vt -шум, который будем считать белым с дисперсией а2.
Пусть, как и выше, S = {Sn)nL-N/2 " " ДПФ от произведения сигнала s на окно Ханнинга w, делённое на N. В оценку параметров модели сигнал входит через величины У = col(YA,YB), где YA = (YA)f=_M, YB = (YkB) =_M, N/2-l N/2-1 Yk= Y SnPn(kF), Yk B = SnQn(kF). n=-N/2 n=-N/2 Минимум среднего квадрата невязки сигнала и модели равен N/2-l Jmin = l Y. tSt-Y R-lY: t=-N/2 причём матрица R не зависит от случайных шумов v. Выделим в векторе Y случайную и детерминированную составляющие. Для этого введём обозначение для идеальной части сигнала: S+ —— J2 (ake Fkt + bk Fkt) так что измеряемый сигнал распадается на детерминированную и случайную части: st = st+ vt, -N/2 t N/2 - 1. В силу равенства Парсеваля запишем компоненты вектора Y во временной области и разделим их на детерминированную и случайную части:
Второе слагаемое в скобках отражает долю шума, скомпенсированного при подстройке модели по данным измерений. Эта доля далее будет вычислена аналитически. После приведения к общему знаменателю получаем формулу в заключении леммы. Формулы для u B(f) и u (f) следуют из их определений. Для доказательства скорости сходимости приведём к общему знаменателю полученное выражение для uff(f). Это рациональная функция, содержащая синусы, аргументы которых определяются дробью f/N. Предельная функция имеет порядок малости С(/"9) при / - схэ. Поэтому можно применить рассуждение из доказательства леммы 1, которое которое понижает степень / на 2 и добавляет N 2.
Подавляемая часть шума определяется величиной tr R lW/N, где обе матрицы имеют размер 2(2М + 1). По лемме 6 первые столбцы тёплицевых подматриц матрицы W имеют конечные пределы при N - схэ. Матрица R аппроксимируется матрицей R в обозначениях теоремы 1. Определим аналогичную аппроксимацию для матрицы W:
Частнвш случай
В предыдущем разделе были описаны способы оценивания целого значения периода основного тона. Далее необходимо уточнить оценку периода для точного вычисления частот старших гармоник голосового сигнала, а также найти все комплексные амплитуды.
Комплексные амплитуды определяются из тёплицевой системы линейных уравнений. Метод простой итерации для решения этой системы обсуждается в первом подразделе. Метод Ньютона для уточнения периода основного тона описан во втором разделе.
Основную вычислительную сложность расчёта параметров аффинной модели составляет решение системы уравнений рв = у, (р 0PQ\ (VA\ (QA\ 0PQ 0Q vB 9B относительно вектора в. На главной диагонали матриц стоят 1. Выделим остальные элементы в матрицы 9Р и gQ: ( пР nPQ\ PQ Q Матрицы gp и gQ тёплицевы и самосопряжённые. Матрица g = p-I самосопряжённая. Исходное уравнение можно записать в виде 9 = у-дв, М=10 М=100
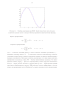
Норма матрицы д в методе простой итерации. пригодном для применения итеративного способа решения, известного как метод простой итерации: в{п+1) = у-дв{п) с начальным данным 0(0) = 0. Метод простой итерации сходится тогда и только тогда, когда спектральный радиус матрицы д меньше 1. В данном случае этот спектральный радиус совпадает с \\д\\.
Матрица д полностью определяется частотой F = N/P и размерностью М, где Р -период основного тона в модели. График зависимости \\д\\ от F приведён на рис. 2.13 для М = 10 и М = 100. Нетрудно видеть, что этот показатель практически не зависит от М.
Метод простой итерации обеспечивает относительную точность 10-3 за одну итерацию при F 3.6. При F 3.6 количество итераций n(F), достаточных для достижения точности ю-3, определяется формулой n(F) = [1.93 - 2.5 (F - 3.6) + 11.5 (F - 3.6)2], F Є [2.8, 3.6], где [] — целая часть числа. При F 2.8 точность оценки аффинного дрейфа по всем гармоникам настолько низка, что лучше применять аппроксимацию стационарной моделью без дрейфа комплексных амплитуд. В стационарной модели уравнение ррЄА = УА решается методом простой итерации 9л(п + 1) = у-дрвл(п) Норма матрицы др в методе простой итерации в стационарном случае. с начальным данным ЄА(0) = 0. График зависимости \\др\\ от F приведён на рис. 2.14 для М = 10 и М = 100. Он практически не зависит от М.
Метод простой итерации сходится, так как норма матрицы др меньше 1. При F 2.8 относительная точность решения системы 10-3 достигается за одну итерацию. При F 2.8 количество ns(F), достаточное для достижения точности 10-3, определяется формулой ns(F) = [1.25 - 9.8 (F - 2.8) - 18.1 (F - 2.8)2 - 16.8 (F - 2.8)3], F Є [1.6, 2.8], где [] — целая часть числа. При F 1.6 точность оценки комплексных амплитуд слишком ненадёжна.
В результате расчёта показателя качества c?2(F) для целых значений периодов основного тона Р = N/F определяются точки локальных минимумов. Для каждой из этих точек требуется рассчитать ближайший локальный минимум a2(F) уже по всем непрерывным значениям F.
Предположим, что в окрестности О заданной точки F0 функция Jmin(F) гладкая и выпуклая. Как правило, окрестность определяется соседними целыми значениями периода основного тона: О = [1/(Р0 + 1), 1/(Д) - 1)], где Р0 = N/F0. Множитель 1/(1 — \/F) практически не меняется в окрестности О точки FQ, поэтому вместо c?2(F) достаточно минимизировать функционал N/2-1 Jmin(F) = S0- Y(F) R-lY(F) - min, S0 = - J] (wtst)2: t=-N/2 или, что то же самое, максимизировать функционал G(F) = Q(F) Y(F) = Y(FYR(F)-lY(F) - max. FeC, где Є = R lY й — вектор оценок комплексных амплитуд гармоник модели. Применим метод Ньютона. Начальное приближение: F = F0. Далее, при каждом п О Fn+i = Pro Fn - " , где Pro — проекция на замыкание окрестности О. Требуется вычислить первую и вторую производные функции G. Первая производная: G = 2Re(e Y )-e R e: так как Вторая производная: G" = 2Re(e y") + 2(У ) Д_1 " - 4ІІе(Є Д/ІГ1У/) + 2Q E!R-1E!Q - Є Д"Є. Введём вспомогательные вектор-функции Zra(F) = {Z(F))%L_M равенством к\ ) N Z Ч дг t=-N/2 Очевидно, что (Z%) (F) = -2irikZ+1(F), -M k M, n = 0,l,... По определению, вектор Y состоит из векторов Y A и Y B с компонентами N/2-1 N/2-1 n=-N/2 t=-N/2 N/2-l N/2-l n=-N/2 t=-N/2 Отсюда производные по F от векторов У"4 и YB вычисляются следующим образом: (XkA) (F) = (Zky(F) = (-2mk)Zl(F): (YkBy(F) = (Ziy(F) = (-2mk)Z2k(F): (YkA)"(F) = (Zk)"(F) = (-i7r2k2)Z2k(F): (YkBY(F) = (ZlY(F) = (-i7r2k2)Z3k(F). Матрица R = R(F) состоит из блоков RP(F) RpQ(F) RpQ(F) RQ{F) RP(F) RpQ(FY R(F) RPQ(F) RQ(F) Матрицы RP(F), RPQ(F) и RQ(F), а также из первые и вторые производные по F тёплицевы и самосопряжённые. Введём обозначения xn(f) = wHiv) e ft n = o,i,... Производные вычисляются по правилу (Xn)\f) = -27гІХп+ЛЛ, П = 0,1,... Элементы матриц RP(F), RpQ(F) и E9(F) можно выразить следующим образом: RL(F) = xo((k-m)F): RkS(F) = X?{{k-m)F), Rkm(F) = X?{{k-m)F). Первые производные: (RL) (F) = -2Tri(k-m)X?((k-m)F): (Rk) (F) = -2in(k-m)X?((k-m)F): (Rkm) (F) = -27n(k-m)X ((k-m)F). Аналогично, вторые производные:
Остаётся найти способ вычисления функций Х (/) при га = 0,1, 2, 3, 4. При га = 0,1, 2 эти функции уже были вычислены, так как они равны, соответственно, гр(/), TPQ{J) и TQ{J). В частности,
Сравнение с существующими алгоритмами определения ЧОТ
Точность оценивания функции ф0 сравнивается с нормой вектора sw = (sWtt) Nl/2. По определению, !st = sw tWt = stwf, где {wt)tlS /2 — окно Ханнинга. Найдём минимальное число Л 0, для которого N/2-1 L +fJ Y 7p( )is;i i?t + 2 Y \ t-gp\ MKW2 t=-N/2+l \ q=l J для любого сигнала s. Левая часть является квадратичной формой, обозначим её f(sw). Искомое число Л есть норма матрицы этой квадратичной формы.
Форма f(sw) обладает рядом особенностей, упрощающих её исследование. Сумму можно переставить таким образом, чтобы в каждом слагаемом оказались произведения сигналов с индексами из одного класса эквивалентности по модулю Р. Выполним это преобразование.
Для каждого вычета к = 0,1,..., Р — 1 минимальное число из промежутка — N/2 + 1 t N/2—1, сравнимое с к, обозначим tk, а количество чисел из этого промежутка, сравнимых Отсюда видно, что исходная задача гарантированного оценивания распадается на Р незави-симых подзадач: Wfc-l ra=0 п Nk-1 stok+nP + 2 2 stok+{n_q)P Afc Y g=l n=0 w,tl+nP 0 к P - 1. Затем в качестве общего множителя Л можно гарантированно выбрать наибольшее из Хк, которое затем максимизируетс и по Р. В практических задачах можно выбирать и взвешенное среднее значений \к с учётом интенсивностей сигнала.
Каждая частная задача решается при помощи следующей леммы, в которую подставляется хп = sto+raP, сп = wto+nP, dn = 7Р( + пР), N = Nk - 1.
Лемма 17. Пусть заданы положительные числа (сп)%=0 и (dn)%=0. Минимальное значение А, для которого
Выполним замену переменной xn = cnyn. Тогда неравенство в лемме равносильно следующе му: У Ау Х\\у\\2. Матрица А самосопряжённая по построению, поэтому минимальное значение А совпадает с \\А\\.п Если Р N/3, что предполагается в постановке задаче, то Nk 2 при всех к и Р. Таким образом, лемму 17 надо применить для случаев N = О, N = 1 и N = 2. В первых двух случаях задача решается аналитически. В последнем случае получается кубическое уравнение, для которого можно подобрать аналитическое приближённое решение.
В итоге, можно сформулировать следующее утверждение Теорема 10. Для каждого Р Є [Pmin, Pmax] \ф0(Р)-фо(Р)\ \\\8ш\\2; где А = max Afc, Afc = IIAll, = c;c7dmaxii i}, 0 i,j Nk-l, 0 k P-l l и Cn = wtok+nP, dn = 7P (tk + nP). 118 Глава 4. Экспериментальные результаты
Предложенный алгоритм оценивания ЧОТ назван «метод минимизации дисперсии шума» (МДШ), или «Noise Variance Minimization» (NVM). На основе полученных результатов создана реализация алгоритма поиска ЧОТ в пакете прикладных программ Matlab [72]. Экс-периментальная проверка показала возможность применения результатов к решению прикладных задач.
В текущей главе продемонстрированы результаты работы алгоритма, а так же сравнение с существующими алгоритмами оценивания ЧОТ.
Сверхточное определение значения ЧОТ является специальной задачей, избыточной во многих приложениях. Так как в полигармонических моделях речевого сигнала частоты входящих в неё гармоник кратны ЧОТ, то и ошибка, возникающая при определении ЧОТ кратно распространяется на старшие гармоники. На рис. 4.1 представлены: участок спектра исходного сигнала, участок спектра восстановленного сигнала с точным значением ЧОТ и участок спектра восстановленного сигнала, где ошибка определения ЧОТ равна 1Гц.
Хорошо видно, что ошибка в 1Гц значительно смещает положение кратных гармоник. В области частот начиная от 4кГц восстановленный и исходный сигналы уже совершенно не похожи друг на друга.
Продемонстрируем все шаги работы алгоритма быстрого оценивания ЧОТ на конкретном сигнале. В качестве примера возьмём участок голосового сигнала (рис. 4.2). спектр исходного сигнала точная оценка ЧОТ неточная оценка ЧОТ Стоит отметить, что сложность алгоритма напрямую зависит от выбора множества М (следствие 3). При выборе Мі и Мг сложность двух вариантов алгоритмов совпадает.
Следующий шаг - приближённое вычисление фо(Р). На рис. 4.3 показана реальная ошибка приближения этой функции, а так же аналитические оценки ошибки, представленные в теореме 9 и теореме 10. Видно, что для множества Мг оценки погрешности в области низких F на порядок ниже, чем для М\.
На следующем шаге осуществим переход от ф0 к Jmin за счёт умножения на соответствующий коэффициент (см. рис. 2.9). На рис. 4.4 показана аппроксимация для Jmin, а так же аналитические границы погрешности для наборов М\ и Мг. Хотя в этом конкретном примере фактическая точность аппроксимации для обоих случаев является более чем допустимой, но аналитическая оценка погрешности разнится сильно.