Содержание к диссертации
Введение
1 Кинетическое уравнение мицеллообразования и термодина мические модели агрегативного равновесия 8
1.1 Сферические агрегаты 12
1.2 Цилиндрические агрегаты 14
1.3 Сосуществующие устойчивые сферические и цилиндрические агрегаты 17
1.4 Линеаризованное уравнение Беккера-Дёринга 21
2 Формирование и релаксация сферических мицелл 24
2.1 Мицеллярная релаксация при малых отклонениях от равновесия 24
2.2 Мицеллярная релаксация и мицеллообразование, описываемые нелинейными дискретными уравнениями
2.2.1 Мицеллярная релаксация 33
2.2.2 Мицеллообразование 39
3 Формирование и релаксация цилиндрических мицелл 42
3.1 Релаксация при малых отклонениях от финального равновесия 42
3.2 Мицеллообразование и релаксация при больших отклонениях от равновесия 53
3.2.1 Релаксация при большом начальном избытке ПАВ в агрегатах 53
3.2.2 Мицеллообразование и релаксация при большом начальном избытке мономеров ПАВ 61
4 Агрегация и релаксация в растворах сосуществующих сферических и цилиндрических мицелл 68
4.1 Характерные времена и характерные моды релаксации 69
4.2 Зависимость от полной концентрации ПАВ и сравнение с
предсказаниями аналитической теории 72
4.2.1 Аналитическая кинетическая теория
4.2.2 Медленная релаксация 73
4.2.3 Быстрая релаксация 76
4.2.4 Переход между временами и модами быстрой релаксации 84
4.3 Мицеллообразование и релаксация при сильных начальных отклонениях от равновесия 85
4.3.1 Мицеллообразование при нулевой начальной концентрации агрегатов с п 1 86
4.3.2 Релаксация при большом начальном избытке мономеров 89
4.3.3 Релаксация при большом начальном избытке ПАВ в агрегатах 97
Заключение 104
Литература
- Сосуществующие устойчивые сферические и цилиндрические агрегаты
- Мицеллярная релаксация и мицеллообразование, описываемые нелинейными дискретными уравнениями
- Релаксация при большом начальном избытке ПАВ в агрегатах
- Мицеллообразование и релаксация при сильных начальных отклонениях от равновесия
Сосуществующие устойчивые сферические и цилиндрические агрегаты
Особенностью молекулы ПАВ является наличие у нее гидрофильной и гидрофобной частей. При растворении в полярном растворителе при концентрациях ниже ККМ ПАВ в растворе находится в виде отдельных молекул. С увеличением концентрации молекулы ПАВ собираются в устойчивые сферические агрегаты. Как уже выше отмечалось, это состояние дает выигрыш в свободной энергии. С дальнейшим увеличением концентрации сферические мицеллы, принимая все новые и новые мономеры, приобретают форму эллипсоида, а затем форму цилиндра. Концентрацию, при которой появляются сферические мицеллы называют первой критической концентрацией мицеллообразования (KKMi), а концентрацию, при которой появляются цилиндрические мицеллы - второй критической концентрацией мицеллообразования (ККМ2). Объектом исследования диссертации являются как мицеллярные системы только со сферическими или только с цилиндрическими мицеллами, так и мицеллярные системы с сосуществующими сферическими и цилиндрическими мицеллами.
Предметом исследования являются процессы мицеллообразования и релаксации мицеллярных систем. Особый интерес представляет кинетика релаксационных процессов при сильных отклонениях от равновесия, то есть таких отклонениях, при которых линеаризация уравнения Беккера-Дёринга не дает удовлетворительных результатов.
Как уже выше отмечалось, в зависимости от концентрации и от геометрических параметров молекул ПАВ молекулярные агрегаты могут иметь разную форму. В этой работе будут рассматриваться агрегаты сферической и цилиндрической формы.
В процессе релаксации мицеллярных растворов происходит присоединение и испускание молекулярными агрегатами отдельных молекул ПАВ. Соответствующие этим процессам переходы между агрегатами можно записать следующим образом:
Агрегаты ПАВ в дальнейшем будем называть n-мерами ПАВ, а отдельные молекулы - мономерами ПАВ. Обозначение {п} соответствует агрегату с числом молекул п. Это число ниже будем называть числом агрегации. апС\ - это число мономеров, присоединяемых конкретным агрегатом с числом агрегации п за единицу времени в единице объема раствора с концентрацией мономеров с\. Величина ап имеет смысл вероятности или частоты встречи какого-то конкретного мономера и какого-то конкретного агрегата с числом агрегации п в единице объема за единицу времени. Величина Ъп+\ - вероятность или частота испускания мономера каким-то конкретным агрегатом с числом агрегации п + 1 за единицу времени в единице объема. Величины ап и Ъп будем называть коэффициентами присоединения и испускания, соответственно. Они зависят от температуры и характеристик самого ПАВ и растворителя, но не зависят от концентраций мономеров или агрегатов.
Введем функцию сп распределения агрегатов по числам агрегации. Распределение сп задается набором концентраций n-меров и будет зависеть от времени t и числа агрегации п. С учетом сказанного изменение концентраций агрегатов во времени подчиняется следующему уравнению материального баланса:
Отдельно рассмотрим случай для п = 1. Первое слагаемое в (1.3) имеет смысл полного числа актов слияния мономеров и агрегатов размера {п} в единице объема за единицу времени. Произведение С\Сп имеет смысл числа всевозможных сочетаний пар мономер-агрегат. В случае же соединения мономер-мономер число всевозможных сочетаний представляет собой выражение С\{с\ — 1)/2. При условии высокой концентрации ПАВ в растворе, то есть при с\ 1, пренебрегаем единицей во втором множителе. Получаем, что
Уравнения (1.2) с учетом определения потоков (1.3)-(1.4) называют дискретными кинетическими уравнениями Беккера-Дёринга. Эти уравнения являются основой кинетического описания мицеллообразования и релаксации в мицеллярных растворах.
Уравнения (1.2), вообще говоря, представляют собой бесконечную систему уравнений. Для численного решения нам необходимо оборвать систему на некотором значении N. Пусть {N} - это агрегат, который не может захватывать мономеры, т. е. агрегат максимального размера, тогда поток JAT=0, а уравнение (1.2) при п = N примет вид
Для замыкания системы (1.2), (1.5) необходимо еще одно уравнение, которое получается из закона сохранения ПАВ. Пусть С - полное количество ПАВ в единице объема системы (брутто-концентрация ПАВ). Тогда закон сохранения ПАВ можно представить в виде
Равновесная концентрация агрегатов cn может быть выражена через равновесную концентрацию мономеров с.\ и безразмерную работу образования агрегатов Wn ("работу агрегации"), выраженную в энергетических единицах квТ: где кв - постоянная Больцмана, Т - абсолютная температура раствора, в виде распределения Больцмана сп = Сіехр(-И/П). (1.13) Работа образования Wn зависит от концентрации мономеров и числа агрегации п. Удобно ввести работу образования Wn, которая не зависит от концентрации мономеров с\ в приближении идеального раствора, соотношением Wn = Wn-(n-l)lnCl. (1.14) Здесь предполагается, что концентрация мономеров измеряется в относительных единицах, и работы Wn и Wn просто совпадают при с\ = 1. С помощью (1.14) в равновесии соотношение (1.13) может быть записано в виде:
В данное работе будут рассматриваться концентрации ПАВ равные и выше ККМ. Как уже отмечалось ранее, выделяют две критические концентрации KKMi и ККМ2 . Первая соответствует образованию заметного количества сферических агрегатов, вторая - цилиндрических. Для определения критических концентраций введем степень мицеллизации следующим образом:
Мицеллярная релаксация и мицеллообразование, описываемые нелинейными дискретными уравнениями
При сравнении численного решения уравнений Беккера-Дёринга с экспериментальными данными и аналитической теорией, изучение линеаризованного версии этого уравнения представляет собой самостоятельный интерес. Это уравнение хорошо описывает поведения мицеллярного раствора при малых отклонениях от равновесия, а также позволяет найти характерные времена и моды1 экспоненциальной релаксации к промежуточному квазиравновесию и финальному равновесию [3-8,17,18]. Линеаризованная форма уравнений (1.9)-(1.12) получится, если представить концентрацию агрегатов в виде cn(t) = сп + 5cn(t), где 5cn(t) С сп, и пренебречь слагаемыми, нелинейными по отклонению 5cn(t). В результате получим линеаризованные уравнения Беккера-Дёринга (1.34)-(1.37).
Уравнения (1.34)-(1.37) тем лучше описывают поведение системы, чем строже выполнено неравенство \5cn{t)\/cn С 1. Вопрос области применимости линеаризованных уравнений рассматривался аналитически и численно в работах [3,4,15,18]. Мы уточним эту область путем сравнения с результатами, полученными при численном решении нелинеаризованного уравнения.
Матрицу коэффициентов уравнений (1.34)-(1.37) полезно симметризо-вать, введя новую функцию: 5cn(t) = un(t)y/cn. (1.38) Подставляя (1.38) в (1.34)-(1.37) и переходя к новым функциям un(t): полу хБудем называть такие характерные времена и моды "дискретными". чим систему (1.39)-(1.42)
Собственные значения симметричной матрицы вещественны, а собственные вектора образуют ортогональный базис для любого вектора и(), соответствующего нормированной функции распределения, характеризующей состояние мицеллярной системы. Собственные векторы можно назвать модами мицеллярного состояния, а собственные значения матрицы А -обратными временами, соответствующими этим модам.
В диссертационной работе исследован полный спектр собственных значений матрицы коэффициентов линеаризованных уравнений Беккера-Дёринга и соответствующие моды, описывающие процесс релаксации ми-целлярных растворов неионных ПАВ со сферическими, с цилиндрическими и с сосуществующими сферическими и цилиндрическими мицеллами. Выявлена зависимость данных характеристик системы от концентраций ПАВ при разных моделях работы агрегации и коэффициентов присоединения мономера агрегатом. Также выполнено численное решение нелинейных дифференциальных уравнений Беккера-Дёринга с использованием метода Эйлера. Несмотря на невысокую точность данного метода, он был выбран в связи с большим объемом вычислений, поскольку обладает достаточно высокой скоростью. Точность решения контролировалась проверкой выполнения закона сохранения полного количества ПАВ на каждом шаге вычислений. Анализ погрешности численного счета показал, что точности этого метода достаточно для решения поставленных задач. Все программы были написаны в пакете прикладных программ Матлаб. Было проведено сравнение численного решения с решением, полученным из аналитических теорий. Глава 2
Формирование и релаксация сферических мицелл Материалы этой главы были опубликованы в [49]. Основные результаты докладывались на следующих конференциях: The eighth Liquid Matter Conference (Wien, Austria, 2011), Dubna International Advanced School of Theoretical Physics, XVIth Research Workshop Nucleation Theory and Applications, (Dubna, Russia, 2012).
В этой главе мы рассмотрим мицеллярный раствор, в котором присутствуют только сферические мицеллы. Постановка задачи была представлена в предыдущей главе. Здесь же мы приведем результаты численных и аналитических расчетов, их сравнение и обсуждение. Так как в этой главе рассматриваются только сферические агрегаты, то под ККМ понимается KKMi.
2.1 Мицеллярная релаксация при малых отклонениях от равновесия
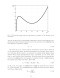
Были рассмотрены малые начальные отклонения от равновесия, то есть считалось, что выполнено условие 5сп(0)/сп С 1 для любого числа агрегации п. Были вычислены собственные значения и собственные вектора матрицы A (1.44)-(1.49) при равновесной концентрации с\ = 1.01 и для модели сферических агрегатов с постоянными коэффициентами ап. Все собственные значения получились отрицательные и невырожденные. Обозначим их Xk и упорядочим по возрастанию абсолютного значения с помощью л
Спектр матрицы линеаризованного кинетического уравнения при с.\ = 1.01. индекса к = 0,1, 2,..., N — 1, как это показано на рис. 2.1. Далее, говоря собственное значение, будем подразумевать абсолютную величину собственного значения. Как видно из рис. 2.1, самое малое собственное значение при к = 0 равно нулю. Оно соответствует закону сохранения полного количества ПАВ в изолированной мицеллярной системе. Следующее собственное значение Ai очень мало, но не ноль. Очевидно, что это самое большое время среди времен релаксации, и оно соответствует обратному времени, которое принято [41,44] называть временем медленной релаксации ts = 1/Ai к финальному равновесию.
Собственные значения при к = 2,3,... заметно больше Ai и соответствуют обратным временам t, = 1/А& релаксации к промежуточному квазиравновесию сферических мицелл в потенциальной яме работы агрегации. Такое промежуточное равновесие устанавливается в конце быстрой релаксации [3,16,44,45,56]. Нетрудно заметить, что собственные значения А& при к 2 расположены почти эквидистантно, рис. 2.1. Время t\ = I/A2 является самым большим среди других характерных времен быстрой релаксации, его обычно называют временем быстрой релаксации tf. Другие времена t\ при к 3 характеризуют более быстрые процессы при быстрой релаксации. Собственные вектора 11 ,11(2) и и 3 матрицы коэффициентов линеаризованных кинетических уравнений (1.39)-(1.42) согласно (1.38) соответствуют 8c1
Релаксационные моды, соответствующие собственнвім векторам матрицві А. релаксационным модам 5сп , 5сп\ 5сп . Эти моды представляют собой вклады в общее поведение отклонения 5cn(t) = X =i Ек ex-p(—\kt)8cn функции распределения от своего равновесного значения. Коэффициенты Ek определяются начальным условием. Эти моды показаны на рис. 2.2. Нетрудно заметить, что с увеличением номера к 1 увеличивается число минимумов и максимумов: при к = 1 имеется один максимум, при к = 2 - один максимум и один минимум, при к = 3 - один максимум и два минимума.
Рассмотрим теперь зависимость собственных значений и собственных векторов матрицы А от равновесной концентрации мономеров с\ и сравним эти зависимости с результатами, полученными при аналитическом решении дифференциального уравнения Беккера-Дёринга. Численные и аналитические зависимости времени релаксации, соответствующего самому маленькому, ненулевому, собственному значению Лі матрицы А, от равновесной концентрации мономеров с\ изображены На рис. 2.3 сплошной линией показаны характерные времена ts = 1/Ai медленной релаксации. Звездочками обозначено медленное время как функция концентрации сі, полученное в [14] с помощью аналитической формулы:
Релаксация при большом начальном избытке ПАВ в агрегатах
Рассмотрим теперь, как зависят полученные результаты от модели скоростей присоединения мономеров к агрегатам. Для этого мы вычислили собственные значения матрицы А при с\ = 1.01, используя в (1.43), (1.44) диффузионную модель кинетических коэффициентов ап: которые задаются выражениями (1.24). Получившиеся результаты оказались весьма близки к тем, что получились при постоянных коэффициентах ап. Это хорошо видно на рис. 2.7(a), где сплошной и пунктирной линией показаны результаты дискретных вычислений времени медленной релаксации ts с постоянными и диффузионными коэффициентами ап (диффузионная кривая нормирована к кривой постоянных коэффициентов множителем 4.7534 при тех же значениях остальных параметров). Символами и 0 обозначены соответствующие результаты, полученные при использовании 2.1, (2.2) аналитической теории. Такая же ситуация наблюдается на рис. 2.7(6) для самого большого времени быстрой релаксации. Сплошной и пунктирной линией представлены результаты дискретных вычислений с постоянными и диффузионными коэффициентами ап: там же символами , 0 (при к=2) и символами х и А (при к=3) обозначены соответствующие результаты, полученные с помощью соотношения (2.7) аналитической теории (здесь диффузионная кривая нор мирована к кривой постоянных коэффициентов с множителем 6.0798 при неизменных остальных параметрах). показывает не только хорошее согласие дискретных вычислений обоих времен релаксаций для разных моделей коэффициентов между собой, но и хорошее согласие с аналитической теорией. Слабую зависимость коэффициента нормировки характерных времен релаксации для разных моделей коэффициентов ап от числа агрегации можно объяснить тем, что общее кинетическое поведение определяется поведением работы Wn вблизи минимума и максимума [17,18], где коэффициенты ап слабо зависят от числа агрегации п. Очевидно, что абсолютные значения характерных времен релаксации, а также отношение времен быстрой и медленной релаксаций будут зависеть от модели коэффициентов.
Рассмотрим теперь релаксацию мицеллярного раствора при концентрациях выше ККМ и при сильном начальном возмущении, требующем решения нелинейных дифференциальных уравнений Беккера-Дёринга (1.9)-(1.12). Получающиеся результаты удобно интерпретировать в терминах нормированной функции распределения An(t):
Отклонение An(t) от единицы означает неравновесное состояние мицеллярного раствора. Если на некотором интервале чисел агрегации п функция Ап перестает зависеть п, то это означает, что в системе установилось квазиравновесное состояние в этой области чисел агрегации. Определим начальное возмущение через нормированную функцию распределения Ап по числам агрегации п в виде МО) = 1 + 16sin (![ ), (2-Ю) так что Ап(0) = 1 при п = 1 и при п равном числу обрезания N. Были численно решены нелинейные уравнения Беккера-Дёринга (1.9)-(1.12) с использованием модели постоянных кинетических коэффициентов t з
Нормированная функция распределения Ага по числам агрегации, концентрация С\ мономеров и относительная концентрация См/см(0) мицелл как функции времени t на различных стадиях нелинейной релаксации (над сплошными линиями для Ап показаны соответствующие времена) для концентрации выше ККМ. ап, работы агрегации (1.17) с параметрами 1.18 и KKMi = 1.01. На рис. 2.8 показана эволюция нормированной функции An(t): концентрации мономеров C\{t) и относительной полной концентрации мицелл См{р)/См{$) (См(0) - это начальная концентрация мицелл при t = 0) на различных стадиях нелинейной релаксации. Приведены также дополнительные графики, проясняющие поведение концентрации мономеров на ранних стадиях релаксации.
Из рис. 2.8 следует, что в интервале времени t = 0 -т-1 происходит формирование плато нормированной функции распределения Ап в области левее горба работы агрегации, что свидетельствует о формировании квазиравновесного распределения в этой области (такое поведение также было обнаружено в [19]). Концентрация мономеров быстро меняется на интервале t = 0 -т- 0.2, но затем это изменение замедляется, полная концентрация мицелл при этом не меняется. Следующая стадия, t = 1-і-250 - стадия быстрой релаксации, на которой происходит обмен веществом между мицеллами путем испускания и поглощения отдельных мономеров, что приводит к формированию плато для Ап в области потенциальной ямы работы агрегации Wn, то есть в этой области формируется квазиравновесное распределение где множитель А определяется текущей концентрацией мицелл См{і)і которая начинает уменьшаться только в конце этой стадии (символ "w" обозначает квазиравновесные величины). Это уменьшение продолжается на последней стадии, t = 250 -і- 5.9 х 106 - стадии медленной релаксации, где наблюдается опускание плато нормированного распределения Ап до значения Ап = 1. Это соответствует установлению финального равновесного состояния мицеллярного раствора.
Мы можем сравнить общую релаксацию концентрации мономеров, полученную при решении нелинейных уравнений Беккера-Дёринга (1.9)-(1.12) с решением линеаризованных уравнений Беккера-Дёринга (1.34)-(1.37) и аналитическими формулами. Это сравнение представлено на рис. 2.9 для двух временных масштабов. В качестве теоретических формул для релаксации на больших масштабах медленной релаксации, мы использовали выражения (1.5) и (1.6) из [15]: t= fCl{t) 7і1/2Апс(смдп3/дСі + 1) ехр(Идп=Пе) Л(о) 1ап\п пАпА1-(см/сі)ещ {\п\п=Па)/тг1/2АпзУ где Сі(0) - квазиравновесная концентрация мономеров, установившаяся в конце стадии быстрой релаксации - показана на рис. 2.9 пунктирной линией. В качестве теоретической формулы для релаксации на меньших масштабах 1.02
Мицеллообразование и релаксация при сильных начальных отклонениях от равновесия
Согласно уравнениям (1.45)-(1.49), все собственные значения матрицы А неположительны и невырождены, как и в случаях систем только со сферическими или только с цилиндрическими мицеллами [49,55], и мы можем их упорядочить по возрастанию абсолютного значения с помощью индекса к как А&, к = 0,1,..., N — 1. Несколько последовательных наименьших абсолютных значений собственных чисел, вычисленных с помощью уравнений (1.15), (1.29), (1.30),(1.31), (1.28) и (1.45)-(1.49) для работы 1, показаны на рис. 4.1. Финальная концентрация мономеров ПАВ принята равной
Как видно из рис. 4.1, наименьшее А& равно нулю и обозначено индексом к = 0. Оно соответствует закону сохранения полного количества ПАВ в единице объема мицеллярного раствора. Следующие два собственных значения Ai и А2 очень малы, но не равны нулю и соответствуют характерным временам релаксации ta\ = 1/Ai и tS2 = I/A2. Очевидно, что эти времена -наибольшие среди всех времен релаксации, и могут быть названы временами медленной релаксации. Так как значения Ai и А2 отличаются более чем на порядок величины (Ai С А2 и ta\ tS2), то существуют две четко отличающихся стадии во время медленного подхода к финальному равновесию. Эти стадии можно назвать первой (с характерным временем ts\) и второй (с характерным временем tS2) стадиями медленной релаксации. Существование двух стадий медленной релаксации является новой особенностью, характерной для систем с сосуществующими сферическими и цилиндрическими мицеллами.
Величины \k с индексами к = 3,4,... соответствуют временам 1/А& релаксации к промежуточному квазиравновесию цилиндрических мицелл при п щ (справа от потенциального горба работы на рис. 1.4). Это промежуточное равновесие устанавливается намного быстрее, чем происходит медленная релаксация, и эту стадию релаксации можно назвать быстрой.
Абсолютные значения собственных чисел матрицы А при релаксации к равно весию при болвших номерах к (для работві 1 и с.\ = (сі)ккм2 = 0.9977). характерных времен быстрой релаксации, и его можно назвать временем tf быстрой релаксации. Другие характерные времена 1/Хк при к 4 характеризуют более быстрые процессы. Величины Xk при к = 3,4,... 9 расположены на рис. 4.1 практически эквидистантно. Таким образом, для этих чисел зависимость собственных значений А& от к почти линейна. Как следует из рис. 4.2, эта линейная зависимость нарушается с ростом номера к при достаточно больших значениях к: и становится квадратичной.
Дополнительную важную информацию о релаксации мицеллярного раствора можно получить из анализа собственных векторов матрицы А. Собственные вектора uSk\ k=0,l,..., N — 1, матрицы А соответствуют модам релаксации дсп неравновесного распределения агрегатов по числам агрегации. Эти моды вносят вклад в общее неравновесное поведение отклонения 5cn(t) = Yl Ekexp(—\kt)5cn концентраций cn(t) от равновесных кон к=\ центраций сп для каждого числа агрегации п (коэффициенты Е\. опреде ляются начальными условиями). Для дискретного спектра А&, все при различных к являются ограниченными функциями числа агрегации п.
Нормированные моды релаксации, соответствующие собственным векторам матрицы А при к = 1, 2, 3, 4, 5 (для работы 1 и Ъ\ = () = 0.9977). сі = (сі)к м2 = 0.9977. Как следует из рис. 4.3, с ростом номера к увеличивается число осцилляции соответствующей моды, и расширяется, занимаемая ими, область чисел агрегации. Наиболее быстро распадаются сильно осциллирующие моды. Быстрая релаксация завершается распадом мо х (з) ды дСп и установлением квазиравновесных состоянии в трех диапазонах
Перейдем к рассмотрению зависимости характерных времен и мод релаксации от брутто-концентрации ПАВ. Будем делать это, одновременно сравнивая результаты с предсказаниями аналитической кинетической теории, основанной на линеаризованном дифференциальном уравнении Беккера-Дёринга. 4.2.1 Аналитическая кинетическая теория
Дифференциальные уравнения Беккера-Дёринга (1.11) в непрерывном пределе п 1 можно преобразовать к дифференциальному уравнению
дсп д_ {
dt дп\(lnClCn
дпСг
(4-і;
Для того, чтобы найти аналитическое решение уравнения (4.1) при полных концентрациях выше ККМ2 , удобно рассмотреть отдельно стадии медленной и быстрой релаксаций. Как мы уже упоминали, быстрая релаксация заканчивается установлением квазиравновесных состояний в области малых предмицеллярных агрегатов с числами агрегации п пс , в области сферических мицелл в диапазоне пс п пс и в облаві сти цилиндрических мицелл с числами агрегации п пс . Аналитическая теория уточняет [39,41,45], что на самом деле квазиравновесное состояние устанавливается в областях с числами агрегации п пс — Апс , пі1» + Дпі1» п п? - Дп? и п п? + Ап?\ где Дп 1» и Дп«2) полуши-рины первого и второго потенциальных горбов работы Wn:
Различия между локальными квазиравновесными состояниями для предмицеллярных агрегатов, сферических и цилиндрических мицелл приводит к появлению прямого и обратного потоков агрегатов через потенциальные горбы работы агрегации. На стадии медленной релаксации эти потоки в областях пс — Апс п пс + Апс и пс — Апс п пс + Апс можно считать квазистационарными.