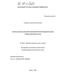Содержание к диссертации
Введение
I. Многочастотное воздействие 23
1. Поведение цилиндрической капли при одночастотном воздействии 24
2. Поведение капли при многочастотном воздействии 37
3. Двухчастотное воздействие, как частный случай много частотного 43
II. Влияние динамики контактной линии 48
1. Деформация капли в вибрационном поле 48
2. Сильно сжатая капля 68
III. Пограничный слой 85
1. Вертикальный пограничный слой 85
2. Пограничный слой на твердой поверхности 97
Заключение 119
Список литературы 123
- Поведение капли при многочастотном воздействии
- Двухчастотное воздействие, как частный случай много частотного
- Сильно сжатая капля
- Пограничный слой на твердой поверхности
Введение к работе
Вибрации являются одним из наиболее распространенных способов воздействия на поведение неоднородных гидродинамических систем. Нетривиальное поведение системы в условиях вибрационного воздействия определяет актуальность теоретического и экспериментального изучения такого рода явлений. Необходимость исследований обусловлена так же тем, что вибрации являются как следствием внешних, посторонних причин, так и могут быть использованы в управлении технологическими процессами.
Собственные колебания. Данная диссертация посвящена изучению воздействия вибраций на неоднородные гидродинамические системы с поверхностью раздела. Исследованию поведения гидродинамической системы при наличии вибраций предшествует изучение собственных колебаний этой системы. В большинстве работ, посвященных изучению систем с поверхностью раздела, рассматриваются малые свободные колебания. Подобные исследования не только важны сами по себе, но и являются начальной ступенью к изучению их нелинейного поведения и под воздействием внешних сил.
В теоретических работах обычно рассматриваются системы с простой геометрией поверхности раздела. Начало этой тематике положили работы Юнга [1] и Лапласа [2]. Одними из первых работ, где исследовались малые свободные капиллярные колебания систем с поверхностями раздела сред относительно их равновесной сферической формы, были работы лорда Рэлея [3-4] и лорда Кельвина [5], изучавших каплю невязкой несжимаемой жидкости. Было показано, что решение можно представить в виде линейной суперпозиции мод с нормальной зависимостью от времени, в основе которых лежат сферические гармоники. Для собственной частоты колебаний была получена формула Рэлея, связывающая частоту с меридиональным числом сферической гармоники и параметрами системы. Механическое равновесие жидкого столба (жидкой зоны) и струи относительно малых свободных капиллярных колебаний теоретически и экспериментально исследовались в работах Платэ [6,7] и лорда Рэлея [8,9].
Именно в этих работах было найдено предельное отношение между высотой жидкого столба L и его радиусом R: L = 2TVR . При больших высотах столб становится неустойчивым и разрушается. Это явление получило название неустойчивости Рэлея. Так же в работе Рэлея [8] рассматривается неустойчивость цилиндрической струи, окруженной другой жидкостью. Собственные частоты свободного жидкого столба можно найти в книге Ламба[10].
В последнее время интерес к подобным конфигурациям вызван их использованием в различных технологических процессах. Например, жидкая зона рассматривается при изучении процессов роста полупроводниковых кристаллов [11,12]. Основное внимание в таких работах уделяется течению внутри жидкой зоны при наличии нагрева, вертикальных вибраций, магнитного поля. Также рассматривалась фильтрация через пористую среду [13,14]. Отметим, что подавляющее большинство работ посвящено рассмотрению цилиндрического жидкого столба (жидкой зоны) окруженного газом, влияние которого не учитывается. Таким образом, боковая Р поверхность столба рассматривается как свободная. Жидкость с малой вязкостью рассмотрена в [10], где найдено приближенное выражение для декремента затухания свободных колебаний сферической капли. В качестве первого приближения им использовалось решение для невязкого случая, на основе которого определялась вязкая диссипация в объеме жидкости. Случай произвольной вязкости жидкости был исследован в работе [15]; подробное описание может быть найдено в книге [16].
Задачу о колебаниях сферической невязкой несжимаемой жидкости, взвешенной в невязкой несжимаемой жидкости другой плотности, можно найти в [10]. В работе [17] получено дисперсионное соотношение для случая произвольной вязкости жидкостей и поверхности раздела жидкостей, обладающей вязко-эластическими свойствами типа Буссинеска - Скривена -Бупара, а также рассмотрен ряд важных предельных случаев.
Та часть работы [17], которая касается влияния вязко-эластических свойств поверхности раздела жидкостей, предварялась исследованиями, приведенными в [10], который рассмотрел колебания сферической капли маловязкой несжимаемой жидкости, покрытой нерастяжимой пленкой, и аналогичной работой [18] о пузыре, отделенном нерастяжимой пленкой от неограниченного объема несжимаемой жидкости малой вязкости. В обоих случаях было найдено, что нерастяжимая пленка на поверхности жидкости существенно увеличивает декремент затухания колебаний. В работе [17] показано, что результаты для нерастяжимой пленки могут быть получены, если считать, что дилатационная вязкость или дилатационная эластичность поверхности раздела жидкостей велики.
Однако авторы [17], не представили иллюстраций численных расчетов спектра собственных частот (а по одним лишь предельным случаям трудно судить об общем характере зависимости собственных частот от параметров системы) и упустили из рассмотрения случай непрерывного спектра собственных частот. Как показано в [19], непрерывный спектр, заполняет область положительных значений декремента затухания, а соответствующие ему апериодически затухающие собственные решения существуют при любых параметрах системы. Там же были приведены графики, иллюстрирующие характер зависимости собственных частот от параметров системы, тем самым его работа дополняет работу [17].
Частоты осесимметричной моды и коэффициенты затухания собственных малоамплитудных колебаний найдены в работе [20]. Рассматривались большие, но конечные числа Рейнольдса. Затухание было вызвано учетом вязкого пограничного слоя на твердых поверхностях. Частоты и коэффициенты затухания осесимметричной и трансляционной моды собственных колебаний вязкой жидкой зоны в поле тяжести были найдены в работе [21]. В этих работах было показано, что значения частот и коэффициентов затухания увеличиваются с увеличением радиуса капли и уменьшаются при увеличении числа Бонда.
Во всех вышеупомянутых работах рассматривались решения с отделенной временной переменной, так называемые нормальные моды, собственные частоты которых находились из проблемы собственных значений. Оставлялись без внимания переходные решения, которые формально можно получить как линейную суперпозицию нормальных мод, но которые, как целое, обнаруживают иное поведение во времени, чем каждая нормальная мода в отдельности, лишь асимптотически приближаясь к наименее затухающей нормальной моде. Кроме того, анализ нормальных мод не решает вопроса о начальной генерации завихренности поля скорости жидкости, например для системы, которая приводится в движение из состояния покоя. Задача Коши для малых свободных капиллярных колебаний сферической в равновесии капли несжимаемой жидкости, взвешенной в несжимаемой жидкости другой плотности и вязкости, была рассмотрена в [22]. В работе [23] были рассмотрены частные случаи капли жидкости в вакууме и пузыря в объеме жидкости, преимущество которых состоит в том, что они допускают аналитическое решение в виде дифференциального уравнения, содержащего обратное преобразование Лапласа [23], или интегро-дифференциального уравнения [24].
В настоящее время большое распространение получили и активно развиваются методы определения физических параметров жидкости (коэффициент поверхностного натяжения, плотность, коэффициент вязкости и т.п.) по характеристикам свободных колебаний их систем. Например, в [25,26] проводились измерения поверхностного натяжения и вязкости капли жидкости, которая левитировала в другой жидкости с помощью звуковых волн. Акустические волны служат не только для «подвешивания» капли в несмешивающейся жидкости, но и для возбуждения колебаний. Благодаря хорошему согласию с линейной теорией, такая методика используется довольно часто [21].
Так, одним из методов определения коэффициента поверхностного натяжения является измерение частот собственных капиллярных колебаний капли жидкости, см., например, [27,28]. Если капля имеет в равновесии сферическую форму, амплитуда колебаний много меньше размера капли, и жидкость невязкая и несжимаемая, то коэффициент поверхностного натяжения может быть вычислен по формуле Рэлея [3]. Различные факторы могут привести к отклонению частот, рассчитанных по формуле Релея при заданном коэффициенте поверхностного натяжения, от реально наблюдаемых собственных частот. В литературе рассмотрены следующие причины изменения спектра частот: вращение капли жидкости [29]; несферичность формы капли [30]; влияние поля, подвешивающего каплю в поле силы тяжести [31,32]; конечность амплитуды колебаний [33,34]; влияние вязкой диссипации [15]. Требование как можно более точного определения коэффициента поверхностного натяжения обуславливает необходимость уточнения формулы Релея. Часто подобное уточнение не может быть получено в замкнутой аналитической форме, что обусловливает применение методов теории возмущений и численных методов.
С помощью измерения частот свободных капиллярных колебаний может быть определено также поверхностное натяжение на поверхности раздела двух несмешивающихся жидкостей. Для этого можно рассмотреть двухслойную систему, которая в равновесии имеет вид жидкой сферической капли, окруженной концентрическим сферическим слоем другой жидкости, что проделано в работах [35,36]. Теоретический анализ нормальных мод малых свободных капиллярных колебаний в такой системе для случая невязких несжимаемых жидкостей, а также экспериментальные наблюдения были выполнены в работе [37]. Для каждого меридионального числа они нашли две моды свободных колебаний с двумя значениями собственных частот, которые являются двумя решениями некоторого биквадратного уравнения. Рассматривались предельные случаи: капли жидкости в вакууме; твердой внутренней капли; поверхности внешней жидкости, граничащей с твердой оболочкой; тонкого или толстого слоя внешней жидкости. Такая же система, но для случая несжимаемых жидкостей высокой вязкости была рассмотрена в работе [38], где было найдено приближенное выражение для декремента апериодического затухания колебаний.
Подобные методы сложно развить на основе исследований жидкой зоны, т.к. в этой конфигурации не возможно рассматривать каплю изолированной. С другой стороны, существующие методы определения физических параметров не работают при высоких температурах, а имеющиеся данные очень неточные. Например, при процессе роста полупроводникового " кристалла методом плавающей зоны, температура расплава составляет 1000 — 3000°С [39,40]. Поэтому в таких случаях, параметры жидкости (расплава) пытаются определить, изучая поведение капиллярных волн на свободной поверхности жидкой зоны [21]. Есть надежда, что, получив в эксперименте частоты и время затухания таких волн, можно определить вязкость и поверхностное натяжение. В работе [41] рассматривалась возможность применения жидкой зоны для определения микро-ускорений при проведении экспериментов по выращиванию кристаллов на борту спутников и космических станций.
Вынужденные колебания. При исследовании систем с поверхностями раздела сред при наличии вибрационного воздействия особое внимание уделяется резонансным явлениям.
Первые работы по этой тематике принадлежат Фарадею, который при рассмотрении влияния одночастотных вертикальных вибраций на горизонтальную границу раздела жидкость - газ экспериментально обнаружил и описал явления возбуждения параметрических колебаний границы раздела (так называемая «рябь Фарадея» или «волны Фарадея») [42].
Теоретическое объяснение этого явления для данной системы было дано в [43] (см. также [44]) с использованием линейного анализа устойчивости для невязкого потенциального течения. Было показано, что уравнения, определяющие поведение системы, эквивалентны системе уравнений Матье, которые исследовались с помощью теории Флоке [45]. Учет малой вязкости производился на основе невязкого течения, то есть путем добавления диссипативного слагаемого в уравнение Матье или вязкого слагаемого в уравнение Бернулли. Полученное дисперсионное соотношение приводило к результатам, согласующимся с экспериментами для маловязких жидкостей [46]. Однако, как показано в работе [47], где на основе полных уравнений выполнен анализ Флоке устойчивости плоской горизонтальной поверхности раздела двух вязких несжимаемых жидкостей, метод Ламба в данном случае не применим, так как существенной становится вязкая диссипация в пограничных слоях, окружающих поверхность раздела, которую этот метод не учитывает. В работе [48], в которой сравниваются и анализируются уравнения Матье для невязкой, слабовязкой и вязкой жидкости. Нелинейная теория возбуждения параметрической неустойчивости для случая малой вязкости жидкости рассмотрена в работе [49].
Горизонтальная граница раздела при вертикальных вибрациях многократно исследовалась в лабораторных экспериментах [50,51] в которых образовывались рельефы на поверхности жидкости как схожие с конвективными структурами (полосы, квадраты, гексагоны, спирали), так и необычные структуры типа треугольников и пр. [52]. В работе [53] было найдено, что при высоких частотах вибраций основным эффектом является сжатие капли вдоль направления оси вибраций, причем этот эффект имеет место как для тяжелой, так и для легкой капли. При двухчастотном (частоты были близки между собой) акустическом взвешивании сферической капли [54,55] наблюдались похожие явления: капля сжималась вдоль вертикальной оси и окончательно принимала форму яблока (dog-bone form). Если разность частот акустического поля была близка к частоте квадрупольной моды собственных колебаний, то происходило резонансное возбуждение квадрупольных колебаний капли. Как показано в [54], это резонанс вынужденных колебаний, а не параметрический резонанс. В работе [56], как и в предыдущей работе, экспериментально исследовалось поведение капель жидкости в одночастотном акустическом поле. Но в отличие от указанных выше работ, исследовался также процесс разрушения капли. Особое внимание уделялось изменению равновесной формы капли при изменении величины акустического давления и механизма разрушения кали в интенсивном акустическом поле. Когда отношение экваториального и равновесного радиуса составляло примерно 1.3, то капля представляла собой фактически плоский диск. На поверхности этого диска параметрическим образом возбуждалась рябь, вызванная взаимодействием двух основных волн, одна из которых движется в радиальном направлении, а другая в азимутальном. Однако эта неустойчивость имеет природу отличную от параметрической неустойчивости Фарадея.
При исследовании поведения цилиндрической капли несжимаемой невязкой жидкости между двумя твердыми поверхностями в одночастотном вибрационном поле [57] был получен для средней формы эффект аналогичный [53]: капля сжималась вдоль оси вибраций независимо от соотношения плотностей. Необычное поведение капель было обнаружено в экспериментах, описанных в работе [58]: тяжелая капля вытягивалась вдоль оси вибраций, а легкая сжималась.
Параметрический резонанс, обнаруженный в [42], наступал в случае равенства внешней частоты удвоенной частоте собственных колебаний o) = 2Qn, со - частота вибраций, Q„ - частота п -моды собственных колебаний. Это результат линейного (по амплитуде вибраций) анализа неустойчивости [43,59,60]. При исследовании нелинейного поведения и анализа устойчивости во втором порядке вводят в рассмотрение еще одну моду собственных колебаний Qm. Можно классифицировать соотношением частот 2-х мод форму поверхности, образуемую параметрическим возбуждением волн Фарадея (так называемые внутренние резонансы) [46]. Свойства системы подбирают так, чтобы отношение частот Qn и Пт этих двух мод составляло определенную величину. Например, в [61] рассматривался случай, когда соотношение частот 1:1, а в [62] 1:2 как наиболее опасные в случае полубесконечного слоя жидкости. В работе [63] в слое конечной глубины рассматривалась неустойчивость в третьем порядке при соотношении частот 1:3, которые для такого случая становиться более опасными, чем рассмотренные в предыдущих работах.
В [64], в отличие от большинства работ, рассматривалась амплитуда вибраций поверхности и объема сравнимая с размерами газового пузыря при одночастотном воздействии. Основная цель работы заключалась в исследовании нелинейного взаимодействия между осцилляциями объема и формы поверхности пузыря, которые возникали или из-за деформации формы или при неравновесном состоянии объема. Для пузырей сферической формы рассматривалось условие резонанса 2:1, для имеющих несферическую форму 1:1 и 2:1, т.е. Q0=Qm или Q0=2Qm (результат малоамплитудного приближения), где Q0 - частота радиальной моды собственных колебаний, От - частота т - ой моды собственных колебаний формы.
В работе [65] исследована параметрическая неустойчивость вынужденных колебаний формы почти сферической капли; показано, что для главных резонансов неустойчивость появляется при выполнении условия синхронизма ct) = Qn + Q.n+l, со - частота вибраций, Q-, Пя+1 - частоты двух соседних мод собственных колебаний. Такое условие резонанса связано с тем, что моды собственных колебаний взаимодействуют через трансляционную моду.
В книгах [66-68] описано явление супергармонического (или нелинейного, в терминах [69]) резонанса в механических системах, который возникает при условии 2co = Qm т.е. при равенстве частоты вибраций (fa половине частоты собственных колебаний. В работе [57] было обнаружено подобное явление: возникал нелинейный резонанс при равенстве внешней частоты половине частоты основной моды собственных колебаний цилиндрической капли. В [70] рассматривался линейный u? = Q, супергармонический 2со = Сї и параметрический резонанс со = 2Q при исследовании колебаний в нелинейной механической системе с одной степенью свободы. Рассматривалось влияние различных параметров на устойчивость системы и появление резонансных колебаний.
Задачам с многочастотным внешним вибрационным воздействием в последнее время уделяется пристальное внимание. При экспериментальном изучении волн Фарадея в [71] при использовании двух кратных частот (та) и псо) вибраций были получены новые необычные рельефы поверхности при наличии внутренних резонансов т:п=4:5 и 6:7, Теоретическое объяснение этих экспериментов дано в [72].
В [73] использовалось рассеивание акустической модулированной волны с несущей частотой а?1 и модуляционной частотой со на поверхности газового пузырька для измерения его размеров и плотности. Если постепенно приближать частоту а к частоте собственных колебаний, то амплитуда колебаний стенок пузырька нарастает и достигает максимума при частотах колебаний стенок cot±cop (линейный резонанс). В [74] рассматривался
параметрический резонанс йЗі±сорІ2 в подобной системе.
В [75] на примере уравнения Дуффинга рассматривалась устойчивость системы с двумя положениями равновесия при двухчастотном вибрационном воздействии с большой и маленькой частотой. Проводились сравнения с поведением такой же системы под действием низкочастотных вибраций и наложением высокочастотного шума.
В [76] изучалось поведение системы с двумя степенями свободы и с квадратичной и кубической нелинейностью при двухчастотном внешнем воздействии. Рассматривались два случая: в отсутствии внутреннего резонанса и с различными возможностями внутреннего резонанса (1:1, 2:1, 3:1, 1:2, 1:3). В [77] исследовался линейный резонанс нелинейного пружинного маятника при внешнем двухчастотном воздействии. Такая система, например, может моделировать поперечную качку судна. Приведена зависимость роста резонансной амплитуды от параметров системы.
Работа [78] посвящена поведению нелинейного осциллятора при многочастотном воздействии. Рассматривались три случая: (1) внешние частоты далеки друг от друга, но близки к собственной частоте осциллятора, (2) внешние частоты близки друг к другу, но далеки от собственной частоты, (3) внешние частоты близки друг к другу и собственной частоте. Исследовалась устойчивость вынужденных колебаний, рассматривалась влияние вязкости и параметра расстройки частоты. Работа [79] посвящена основным формам нелинейных колебаний вибрационной системы с одной степенью свободы и нелинейностью второго, третьего и четвертого порядка при внешнем многочастотном гармоническом воздействии. Рассмотрены линейный, параметрический и супергармонический резонансы. Рассматривалось влияние нелинейностей на поведение системы. Изучалась возможность управления и подавления нелинейного резонанса.
Влияние малой вязкости жидкостей исследовалось в работе [65,80] феноменологически, искусственным добавлением в амплитудные уравнения членов, отвечающих за диссипацию энергии, что приводит к появлению конечного порога по амплитуде вибраций и сдвигу резонансной частоты. Малая вязкость оказывает дестабилизирующее влияние, сдвигая область неустойчивости в область устойчивости для невязкого случая. Было обнаружено, что в случаях нулевой вязкости и вязкости, стремящейся к нулю, области неустойчивости в пространстве параметров "амплитуда вибраций — расстройка частоты вибраций" не совпадают. Подобный эффект был обнаружен и при исследовании параметрической неустойчивости полусферической капли маловязкой жидкости на вибрирующей подложке [81]. В последней работе учесть малой вязкость проводился строго, аналогично [49].
Экспериментально стоячие волны на свободной поверхности вибрирующего жидкого моста впервые рассмотрел [82]. Он же впервые попробовал определить частоты собственных колебаний осесимметричной моды. Подобные эксперименты, выполненные позднее описаны в работах [83,84]. В работах [85,86] экспериментально определялись частоты собственных колебаний жидкого моста окруженного другой жидкостью близкой плотности.
В работе [87] рассматриваются нелинейные вынужденные колебания конечной амплитуды вязкого жидкого моста в поле тяжести, верхний торец которого совершает гармонические колебания. Особое внимание уделялось линейному резонансу на собственных частотах осесимметричной моды. Резонансная частота определялась по максимальному значению отношения коэффициента деформации и амплитуды вибраций. Коэффициент деформации определялся как интеграл по все высоте капли от абсолютного значения отклонения боковой поверхности от равновесной формы. Наблюдается сдвиг частот собственных колебаний в сторону уменьшения по сравнению с линейной теорией [21]. В то же время увеличиваются значения коэффициентов затухания. С ростом амплитуды вибраций уменьшается значение резонансной частоты. Слабо нелинейный анализ осесимметричных вынужденных колебаний моста маловязкой жидкости проведен в работе [88].
В большинстве приведенных выше работ рассматривались несжимаемые жидкости. Подробное описание различных эффектов связанных со сжимаемостью, например, газовых пузырьков, можно найти в обзоре [89].
Динамика контактной линии. Первой работой, посвященной поведению контактного угла, была работа [1], в которой удалось связать значение равновесного краевого угла со значениями свободной энергии поверхностей раздела фаз (фактически, с коэффициентами поверхностного натяжения), не зная ничего о структуре переходной зоны. В этой работе было получено так называемое уравнение Юнга (или уравнение Юнга - Лапласа), которое связывает разность давлений на поверхности раздела и кривизну поверхности. Подобное уравнение независимо получил Лаплас [90,91].
Работы, посвященные поведению контактного угла и движению линии контакта, можно разделить на два типа. В первом рассматривается установившееся движение контактной линии по подложке. Растекание жидкости в этом случае происходит или за счет межчастичного взаимодействия (например, ван-дер-ваальсовое притяжение молекул жидкости к подложке) или за счет статических внешних воздействий (например, сила тяжести). Подробный обзор основных методов и приближений, применяемых в теории смачивания, приведен в [90]. Ранние экспериментальные [92] и теоретические работы [93] посвящены растеканию жидкости при малых капиллярных числах Са. К настоящему времени имеется довольно много экспериментальных работ [94], в которых рассматриваются процессы при более интенсивном движении и при конечных значениях краевого угла.
Ко второму типу принадлежат работы, где рассматриваются высокочастотные колебательные движения контактной линии. В этом случае ситуация коренным образом отличается от рассмотренной выше. В этом случае влияние вязкости играет существенную роль только в тонких пограничных слоях вблизи твердой поверхности, а движение контактной линии определяется в основном быстро осциллирующим полем давления. Таким образом, можно рассматривать невязкое поведение жидкости в ядре, учитывая вязкость лишь внутри динамического пограничного слоя вблизи твердой подложки. Сложные процессы, происходящие в непосредственной близости линии контакта, из рассмотрения исключаются с помощью эффективных граничных условий, накладываемых на динамику видимого краевого угла.
В указанной работе также проводится качественное сравнение с
экспериментальными работами разных авторов. В частности, показано, что заметные расхождения между экспериментальными измеренными и теоретическими рассчитанными (учитывалось только вязкое трение в пограничном слое) декрементами затухания колебаний можно объяснить диссипацией энергии в окрестности контактной линии. При сравнении с результатами экспериментов [96] показано, что шлифовка поверхности увеличивает параметр смачивания от значений порядка единицы до нескольких десятков. Таким образом, параметр Л характеризует не только химические свойства пары материалов жидкость - подложка, но и степень обработки последней.
В работах [97-98] предполагается, что изменение контактной линии может происходить не в фазе с изменением краевого угла, т.е. капиллярный параметр может быть комплексным.
Частоты и коэффициенты затухания осесимметричной моды мало -амплитудных собственных колебаний жидкого моста рассматривались в работе [20]. Динамика контактной линии учитывалась с помощью эффективного граничного условия (1). В тоже время, принималось во внимание существование тонкого вязкого пограничного слоя на твердой поверхности. Контактная линия движется по поверхности погранслоя. Значения частот собственных колебаний уменьшались с ростом капиллярного параметра. Наибольшие частоты имеет жидкий мост с закрепленной контактной линией. С увеличением отношения равновесного радиуса и высоты капли значения частот возрастали. Не до конца остается выясненным вопрос правомерности учета вязкого пограничного слоя на твердой поверхности. Эффективные граничные условия как раз и предназначаются для того, чтобы не рассматривать процессы диссипации в самом пограничном слое.
В работе [104] рассматривались аналогичные режимы поведения капиллярно-гравитационных волн. В малоамплитудном режиме результаты эксперимента хорошо описывались условием (1). Результаты при больших амплитудах объяснялись в рамках моделей [95,98,103] с введением некоторого эффективного капиллярного коэффициента Ле .
В заключении представлены основные выводы и результаты данной диссертации.
Цели работы.
1. Изучение влияние многочастотных мало амплитудных вибраций поперечных вибраций на цилиндрическую каплю невязкой несжимаемой жидкости, окруженную другой жидкостью. Нахождение средней формы капли.
2. Исследование устойчивости вынужденных колебаний цилиндрической капли относительно малых возмущений.
3. Рассмотрение собственных и вынужденных мало амплитудных колебаний цилиндрической капли, помещенной в другую жидкость при учете динамики контактной линии. Нахождение средней формы капли.
4. Изучение влияния вязкого пограничного слоя на поверхности раздела на вынужденные колебания цилиндрической капли. 5. Изучение устойчивости вынужденных колебаний маловязкой цилиндрической капли относительно мало амплитудных возмущений. Научная новизна результатов.
1. Впервые получены выражения, описывающие течение в цилиндрической капле идеальной жидкости и в окружающей ее другой жидкости в мало амплитудном многочастотном вибрационном поле при поперечной вынуждающей силе.
2. Найден нелинейный резонанс вынужденных колебаний. Построена средняя форма капли. Исследована параметрическая неустойчивость вынужденных колебаний относительно малых возмущений. Построена карта устойчивости.
3. Рассмотрены собственные колебания цилиндрической капли, окруженной другой жидкостью, при учете динамики контактного угла. Впервые получены уравнения для нахождения значений частот и коэффициентов затухания собственных малоамплитудных колебаний капли.
4. Изучена зависимость частот и коэффициентов затухания собственных колебаний от капиллярного параметра и отношения геометрических размеров. Показано, что существуют такие значения капиллярного параметра, при которых частоты собственных колебаний могут обращаться в нуль.
5. Найдены выражения, описывающие течение в цилиндрической капле и в окружаЕОщей ее жидкости при учете динамики контактного угла. Найдена средняя форма капли.
6. Рассмотрены собственные и вынужденные колебания сильно сжатой цилиндрической капли. Показано, что существуют три характерные значения собственных частот.
7. Исследована устойчивость вынужденных колебаний цилиндрической т-капли с учетом вязкого пограничного слоя на поверхности раздела при продольных и поперечных вибрациях. Автором представляются к защите:
1. Результаты исследования устойчивости вынужденных колебаний цилиндрической капли идеальной жидкости, окруженной другой жидкостью при поперечных многочастотных вибрациях.
2. Результаты исследования собственных колебаний цилиндрической капли окруженной другой жидкостью при прямом равновесном краевом угле, учете динамики контактной линии и поперечных вибрациях.
3. Частоты и коэффициенты затухания собственных колебаний сильно сжатой цилиндрической капли окруженной другой жидкостью при произвольном равновесном краевом угле, учете динамики контактной линии и поперечных вибрациях.
4. Результаты исследования устойчивости вынужденных колебаний свободно скользящей цилиндрической капли окруженной другой жидкостью при учете вязкого пограничного слоя на поверхности раздела и поперечных вибрациях.
5. Результаты исследования устойчивости вынужденных колебаний цилиндрической капли со свободной поверхностью при продольных и поперечных вибрациях.
Достоверность результатов. Достоверность полученных результатов подтверждается сравнением с известными ранее работами и согласием результатов, полученных разными методами и с использованием разных подходов.
Например, результаты исследований собственных и колебаний цилиндрической капли (при учете динамики краевого угла) хорошо согласуются с ранее полученными результатами для осесимметричной моды.
Публикации. Материалы диссертации изложены 10 работах: [57, 106-114].
Апробация работы. Результаты работы докладывались на XII Зимней школе по механике сплошных сред (Пермь, 1999); VIII Международной конференции "Устойчивость и турбулентность течений гетерогенных и гомогенных жидкостей" (Новосибирск, 2001); XXIX Summer School "Advanced Problems in Mechanics" (Санкт-Петербург, 2001); конференции НОЦ "Неравновесные переходы в сплошных средах" (Пермь, 2002); Всероссийской конференции «Теория и приложения задач со свободными границами» (Бийск, 2002); XIII Зимней школе по механике сплошных сред (Пермь, 2003); XXXI Summer School "Advanced Problems in Mechanics" (Санкт-Петербург, 2003); конференции НОЦ "Неравновесные переходы в сплошных средах" (Пермь, 2003); XXXII Summer School "Advanced Problems in Mechanics" (Санкт-Петербург, 2004), а также на Пермском городском гидродинамическом семинаре имени Г.З. Гершуни и Е.М. Жуховицкого.
Практическая ценность. Полученные результаты могут быть использованы для создания методов изучения физических параметров и свойств жидкости бесконтактным способом. Также они могут быть полезны для изучения поведения различных включений в слое жидкости между твердыми поверхностями при наличии вибраций.
Поведение капли при многочастотном воздействии
Полученное выше решение может оказаться неустойчивым относительно малых возмущений. При мало амплитудном внешнем воздействии возможна только параметрическая неустойчивость. Для нахождения резонансных областей введем возмущения основного состояния в виде: (р = р + у/, = $ + %, p p + q (1.54) где р , \ р — возмущенные поля, р, , р — характеризуют основное решение, i//, t д — малые нестационарные возмущения. Подставляя возмущенные поля (1.54) в исходную систему (1.34) - (1.40) и линеаризуя по возмущениям, получим для возмущений систему уравнений и граничных условий: А = 0, q = -p(y/t + V pVy/) (1.55) г-»оо: у/-»0 (1.56) r = l: [n] = 0 t=S/ F-WgN , M = + - " + 0 + - (1-57) J(l + 2 + V2) cosada = 0 (1.58) о ]%da = -s]&da (1.59) о о Решение системы (1.55) - (1.59) будем искать методом многих масштабов. Напомним, что в работе [65] при изучении устойчивости вынужденных колебаний сферической капли, необходимым условием наступления параметрического резонанс является выполнение для двух соседних мод свободных колебаний: m - ой и т +1 - ой, одного из условий синхронизма: y = nm+Qm+] (1.60) = п«-п„+і (1.61) Авторами [65] было сделано заключение для невязкого случая о том, что, при выполнении второго условия (1.61), параметрический резонанс не возникает при любой малой амплитуде вибраций. Поэтому в данной работе будем рассматривать только условие (1.60). Чтобы описать близость частоты вибраций к сумме Qm + Пт+1 количественно, введем параметр расстройки у — єу -v є1 у2 +..., определив его с помощью соотношения: О + Пт+1 =а-єух-єгуг -... (1.62) Таким образом, в нулевом порядке разложения получаем следующую задачу: Ayl0)=O,qm=-priO) (1.63) r- oo: m- 0 (1.64) r = l: [ 0)] = 0, 0) =Y?\ (в)Н(0)+#? (1.65) решение которой имеет вид: f) = V ( „.yV V + с.с, (1.66) V 0) —Е«— tt-O T V""1 +С.С (1.67) (0) = ХВГ( -" АЛегмог + cc (1.68) где i0 = f, tx=st, символом «с.с.» здесь и далее обозначены комплексно сопряженные слагаемые. В первом порядке получаем следующую задачу Д (1)=0, qw =-р(уМ + )-pVy/wV pm (1.69) г- оо: (1) 0 (1.70) r = l: [ 1 + - =0, + = , (1.71) Полученная краевая задача (1.69) - (1.71) содержит секулярные слагаемые, которые необходимо исключить для получения равномерно пригодного по времени решения. Условие разрешимости дает следующие обыкновенные дифференциальные уравнения: ДВ« + ir,fli =2 (0,- ,) (1.72) га+1 а (0) д«Ц где Д -—. Будем искать решение для амплитуд В{т , 5„ в виде ехр(/Ц) д\ Подставляя это решение в (1.72) - (1.73), получим систему алгебраических уравнений для соответствующих амплитуд. Эта система имеет нетривиальное решение, если ее определитель равен нулю. Из этого условия получаем уравнение для инкремента X (1.74)
В зависимости от знака правой части выражения (1.74) возможно два случая развития малых возмущений. Если правая часть отрицательная, то Я чисто мнимое. При таких инкрементах существуют только колебательные режимы для возмущений. Такие возмущения не возрастают и не затухают. Если правая часть (1.74) положительная, то X действительны. При положительных действительных X возмущения нарастают, а при отрицательных затухают. Если бы собственные частоты Clm, Пт+1 имели разные знаки, то правая часть (1.74) была бы отрицательной. В результате этого, резонанс возможен только на сумме двух частот соседних мод, т.е. когда частоты имеют одинаковые знаки. Именно этот факт не дает возникнуть параметрической неустойчивости при условии (1.61). Переход между действительными и мнимыми инкрементами происходит при Л = 0. Из этого условия можно найти пороговую амплитуду вибраций как функцию параметра расстройки /,. Вид нейтральной кривой є{й)к) определяется выражением: На рис. 1.4. приведены первые две области (для co = Q.2+Q.z и со = П3 + С14) параметрической неустойчивости. Значения частот Qn собственных колебаний вычисляются по формуле (1.51). Обобщим полученные выше результаты на случай многочастотного воздействия. Геометрия задачи аналогична рассмотренной в предыдущем параграфе (см. рис. 1.1). Капля обтекается пульсационным потоком. Центр масс капли движется относительно лабораторной (неподвижной) системы отсчета вдоль оси х со скоростью U(t), которая подлежит определению; жидкость на больших расстояниях от капли движется вдоль оси ж со скоростью: компоненты функции f(f), j - орт вдоль оси х. Амплитуды внешних воздействий Лк малы по сравнению с равновесным радиусом R. Как и в предыдущем параграфе, будем предполагать, что, с одной стороны, частоты вибраций достаточно велики, чтобы можно было пренебречь вязкостью: с другой стороны, частоты вибраций достаточно малы, чтобы можно было пользоваться приближением несжимаемости: Уравнение Эйлера в системе центра масс имеет вид Считая движение безвихревым, введем потенциалы скоростей v = V p. Переходя к безразмерным переменным (выбрав в качестве единиц измерения Условие неподвижности центра масс (1.86) и условие сохранения объема (1.87) выполняются автоматически, Скорость движения центра масс относительно лабораторной системы отсчета: Как и в случае монохроматических вибраций, эта скорость обращается в ноль для очень тяжелой капли, совпадает со скоростью движения окружающей жидкости при р{=ре=1 и больше скорости жидкости на бесконечности для легкой капли (пузыря). В первом порядке получаем задачу:
Уравнение (1.100) получено в ходе решения краевой задачи (1.94) - (1.99). В решение (1.92) предыдущего порядка входят только слагаемые, содержащие QXp(±io)kt). В рассматриваемом порядке решение (1.97) - (1.99), как видно из неоднородного слагаемого уравнения (1.100), зависит от парных комбинаций (сумма или разность) частот вибраций ехр(±г(й)4 іш і). Собственная частота общего решения однородного уравнения (1.100) равна частоте квадрупольной / моды, т.е. п = 2 в (1.51), собственных колебаний капли. Если какая-либо комбинация внешних частот в неоднородном слагаемом (1.100) будет близка к такой частоте, то возникнет явление резонанса. Напомним, что в случае монохроматических вибраций резонансное нарастание амплитуды колебаний капли происходит при частоте, которая вдвое меньше наименьшей частоты собственных. В случае многочастотных вибраций резонанс вынужденных колебаний может возникнуть, как видно из уравнения (1.100), также в случае, когда сумма или разность двух внешних частот равна частоте квадрупольной моды. Независящая от времени часть функции описывает эффект изменения средней формы капли: Угловые скобки обозначают осреднение соответствующей величины по времени. Как видно из (1.101), независимо от соотношения плотностей имеет место эффект сжатия капли вдоль оси вибраций. Полученное выше решение может оказаться неустойчивым относительно малых возмущений. Для нахождения резонансных областей введем возмущения основного состояния в виде: где р\ С Р возмущенные поля, р, , р — характеризугат основное решение, у/, , q -малые нестационарные возмущения. Подставляя возмущенные поля (4.1) в исходную систему (2.11)-(2.12), (2.14)-(2.18) и линеаризуя по возмущениям, получим для возмущений систему уравнений и граничных условий: Решение системы (4.2)-(4.6) будем искать методом многих масштабов, аналогично случаю монохроматических вибраций. Как уже отмечалось выше, при монохроматическом вибрационном воздействии параметрическая неустойчивость для главных резонансов появляется при выполнении условия синхронизма со = Qm + Пга+1. Влияние много частотности никак не скажется на этом условии. Данное условие связано с тем, что основной модой для вынужденных колебаний является трансляционная, а для собственных колебаний — квадрупольная. Таким образом, в нулевом порядке разложения получаем следующую задачу:
Двухчастотное воздействие, как частный случай много частотного
Рассмотрим основные полученные эффекты для конкретного случая внешнего воздействия. Представим размерную функцию f(t) в следующем виде: Безразмерная скорость движения центра масс относительно лабораторной системы отсчета (1.93): Решение (1.92) в нулевом порядке разложения по степеням є с учетом (1.123) примет следующий вид: Решение (1.97) - (1.99) в первом порядке разложения имеет вид: (1.126) Независящая от времени часть функции Q описывает эффект среднего изменения формы капли. Как уже отмечалось выше, независимо от соотношения плотностей, имеет место эффект сжатия капли вдоль оси вибраций. Зависящая от времени часть функции % имеет резонансный характер: амплитуда колебаний капли неограниченно нарастает при приближении частот вибраций к резонансным значениям. Резонансное нарастание амплитуды колебаний может происходить не только на внешней частоте, которая вдвое меньше частоты квадрупольной моды собственных колебаний (супергармонический или нелинейный резонанс), но и в случае равенства суммы или разности внешних частот равных этой частоте. Напомним, что в монохроматическом случае слагаемые содержат только удвоенную частоту вибраций. На рисунке 1.4. показаны изолинии энергии колебаний в зависимости от частот вибраций. При приближении частот к резонансным значениям, амплитуда колебаний нарастает неограниченно, что связано с отсутствием диссипации. Штриховые линии соответствуют резонансам у, ± ео2 ±Q2, w,=fi2/2, fy2=Q2/2. Если рассматривать какую-либо величину, например, давление, то в процессе движения капли давление проходит точку максимума два раза за один период внешнего воздействия. Это связанно с наличием в решении первого порядка (1.126) - (1.128) слагаемых с удвоенными внешними частотами. Таким образом, нелинейный резонанс возникает, когда одна из частот вибраций равняется половине частоты квадрупольной моды собственных колебаний. В первой главе рассмотрены колебания и осредненная деформация цилиндрической капли идеальной жидкости, окруженной другой идеальной жидкостью и находящейся между двумя твердыми поверхностями.
Капля обтекается пульсационным потоком. Предполагается, что среднее искажение капли мало, равновесный краевой угол равен к 12 и не изменяется. Показано, что в главном порядке разложения по амплитуде вибраций форма капли не изменяется и она смещается, как целое (трансляционная мода). Обнаружено явление супергармонического резонанса. Супергармонический (нелинейный) резонанс в многочастотном случае появляется при внешних частотах, равных половине частоты квадрупольнои моды собственных колебаний или при равенстве суммы (или разности) внешних частот собственной частоте. В монохроматическом случае резонанс возникает при совпадении внешней частоты с половиной собственной частоты. Данный резонанс является резонансом на вынужденных колебаниях, в отличие от параметрического резонанса, возникновение которого связано с их неустойчивостью. Найдено, что отклонение средней формы капли от цилиндрической ІК пропорционально квадрату амплитуды вибраций. Имеет место сжатие капли в направлении оси вибраций при любом соотношении плотностей. При высоких внешних частотах средняя форма капли не зависит от выбора системы отсчета. Исследована устойчивость вынужденных колебаний относительно малых возмущений. Показано, что параметрический резонанс появляется при выполнении условия синхронизма: одна из внешних частот равна сумме частот соседних мод собственных колебаний. Найден параметр расстройки и построены области неустойчивости.
При высокочастотном вибрационном воздействии вязкость играет существенную роль только в тонких пограничных слоях вблизи поверхности раздела. Это позволяет рассматривать невязкую жидкость в ядре и вязкую в погранслое. При этом диссипация энергии в вязком погранслое на твердой поверхности существенно больше, чем на поверхности раздела двух жидкостей. Однако учитывать движение контактной линии в таком погранслое очень сложно. Поэтому обычно используют эффективные граничные условия, которые накладываются на динамику контактного угла, что позволяет исключить из рассмотрения все сложные процессы вблизи контактной линии. В данной главе рассматривается влияние динамики контактной линии на собственные и вынужденные колебания цилиндрической капли
Сильно сжатая капля
В предыдущем параграфе равновесный краевой угол между боковой поверхностью капли и твердой поверхностыо был равен я/2. Рассмотрим отсчитывается от нижней твердой поверхности в сторону боковой поверхности капли. В граничном условии 2.11), описывающем динамику контактной линии, необходимо учесть равновесную форму с краевым углом отличным от прямого: Здесь 0 — отклонение формы капли от цилиндрической в состоянии равновесия. Краевой угол «9 и отклонение поверхности связаны соотношением В результате, рассмотренная выше задача (2.7) - (2.11) в рассматриваемом случае, с учетом (2.88) и (2.89), примет вид Равновесная форма жидкой зоны будет определяться условием баланса нормальных напряжений при q = 0; с граничными условиями: отклонения поверхности и давления в ряд по степеням малого параметра fi: найдены частоты собственных колебаний для сильно сжатой капли при прямом равновесном краевом угле. Было показано, что существуют различные масштабы частот и капиллярного параметра. Найдем для начала частоты трансляционной моды собственных колебаний. Соответственно, используемые единицы измерения соответствуют масштабам частот трансляционной моды. Используя разложения (2.102), получим в главном порядке разложения систему уравнений и граничных условий для комплексных амплитуд потенциала, давления и отклонения поверхности в разных областях течения. В капле и во внешней жидкости Воспользуемся методом сращивания для объединения решений (2.107) -(2.109) и (2.116) - (2.118). Согласно этому методу, разложим, например, решение (2.107) вблизи поверхности г = 1 + ДЙ +... и сравним с решением (2.116) pf =c/e/n cosa = c/(l + I))e n/cosa (2.119) Из (2.119) и (2.116), следует, что c0i=cn си рсг Аналогично, с0е = сеУ си = -/?се, с = g. Таким образом, можно объединить задачи и решения Для нахождения амплитуд с,, се, си, с2к gi с4, сгк и собственных чисел задачи О. использовалась обобщенная процедура Галеркина. Согласно этому методу решения (2.126) - (2.128) надо подставить в граничные условия (2.121)-(2.123) , (2.125) и умножить каждое на различные моды. После подстановки (2.126) — (2.127) получим следующую систему уравнений: Проинтегрируем уравнение (2.131) два раза по высоте капли.
После чего, умножив каждое уравнение на базисные функции и проинтегрировав каждое по высоте жидкой зоны, получим Зп +1 независимых алгебраических уравнений для нахождения амплитуд ct, се, с]к, с2к, g, с4, си. При реализации метода Галеркина элементы матриц находились методом численного интегрирования по схеме основанной на правиле Гаусса — Кронрода. В результате получалась обобщенная задача на собственные значения. Условие Det(Q) = 0 позволяет определить собственные числа Q в зависимости от параметров задачи. В случае прямого равновесного краевого угла решение системы (2.129) - (2.132) совпадает с решением (2.51). Полученные частоты Q для различных случаев равновесного краевого угла показаны на рис 2.11 (а, Ъ). На нем представлены вещественная С2Г и мнимая П, (коэффициент затухания) части комплексной собственной частоты С1. Полученное уравнение имеет комплексные решения, что приводит к затуханию колебаний. Это затухание вызвано лишь условием на линии контакта и не связано с вязкостью. Как и в рассмотренном выше случае, для основной частоты трансляционной моды существует характерное значение капиллярного параметра. Нулевая частота трансляционной моды при некотором значении Л обращается в нуль (рис 2.11а).
Этому значению соответствует появление двух веток декрементов затухания (рис. 2.1 lb). При рассмотрении пределе силыюсжатой капли в предыдущей части было показано, что высоким частотам соответствуют волны на поверхности раздела. Эти волны не зависят от медленной радиальной координаты. В случае высоких частот, решение для потенциалов будем искать в виде Как и в предыдущем случае, будем искать решение этой системы методом Галеркина. Комплексные частоты П для 3-х различных случаев равновесного краевого угла показаны на рис. 2.11 (с, d). В случае прямого равновесного краевого угла, уравнение для нахождения частот собственных колебаний совпадает с уравнением (2.48). Низкие частоты соответствуют движению свободно скользящей капли. Такое движение зависит только от медленной радиальной координаты, и не зависит от быстрой радиальной и вертикальной координат.
Пограничный слой на твердой поверхности
Пусть капля жидкости плотностью р окружена газом, плотность и -- -— — -. вязкость которого не оказывает л существенного влияния на поведение — - капли. В результате этого, влияние внешней среды можно не учитывать (рис. 3.5). Контактная линия Рисунок 3.5. Геометрия задачи. Вязкие пограничные слон выделены штриховкой НЄПОДВИЖНа. ДВИЖЄНИЄ капли вызвано колебаниями твердых поверхностей. Вязкость играет существенную роль только на поверхностях раздела в узких пограничных слоях. Поэтому влияние вязкости будем учитывать в пограничном слое на твердой поверхности. Краевой угол в процессе движения изменяется. Предполагается, что амплитуда внешних вибраций А и толщина вязкого пограничного слоя S малы по сравнению с равновесным радиусом R и высотой капли h. Уравнение движения и уравнение непрерывности в системе отсчета связанной с сосудом можно записать следующим образом: На поверхности капли должны выполняться следующие граничные условия: кинематическое 99 нормальных напряжений -р + Jinn = -аV п касательных напряжений Jinf = О боковой поверхности, f - вектор касательной к боковой поверхности. На твердых поверхностях необходимо поставить условия прилипания и непротекания Контактная линия неподвижна Переходя к безразмерным переменным (выбрав в качестве единиц измерения времени J—— длины R, высоты h, скорости АА\——j-, отклонения 1 lv ACT поверхности Л, толщины пограничного слоя —І—, давления —т-, вязкости v, R \ш R плотности р), получаем следующую задачу: Индексы t, r, a, z обозначают дифференцирование по соответствующим переменным. Задача содержит следующие безразмерные параметры: малую амплитуду вибраций є = —, квадрат малой толщины вязкого погранслоя т S2 -—J——, безразмерную частоту внешних вибраций й = ет R отношение равновесного радиуса капли и толщины слоя 6 = —, отношение h малой амплитуды вибраций и малой толщины пограничного слоя s = —. Рассмотрим собственные колебания одиночной капли. Общая задача (3.70) - (3.76) запишется в виде: Как уже отмечалось выше, вязкость оказывает влияние только в пограничном слое, поэтому запишем отдельно задачи для невязкого ядра и вязкого погранслоя.
В пограничном слое скорость и давление жидкостей могут претерпевать значительные изменения в направлении нормальном к поверхности раздела, что требует введения «быстрой» вертикальной координаты для верхнего и нижнего погранслоя, соответственно Решение уравнения Навье — Стокса (3.77) будем искать в виде суммы потенциальной части V p для не вяз кого ядра и вихревой V для вязкого пограничного слоя. Уравнение движения (3.77) будет иметь вид: Решение задачи (3.85)-(3.94) будем искать в виде разложения (3.25) - (3.28) в ряд по малому параметру S. Подставляя разложение (3.25) - (3.28) в (3.85)-(3.94), в главном порядке разложения для невязкого ядра получим следующую задачу: Из граничных условий (3.97) и (3.103) следует, что только касательная к твердой поверхности компонента скорости V0 будет отлична от нуля. В первом порядке разложения для невязкого ядра получается следующая задача Частота ш1 является поправкой к основной частоте Q и связана с наличием процессов диссипации в пограничном слое. Отметим, что нет необходимости находить решение задачи (3.105) — (3.110) для нахождения поправки щ. Потенциалы (р0 и рх являются гармоническими функциями, поэтому можно воспользоваться формулой Грина: где V - объем капли, F - площадь поверхности капли. Решение задачи (3.95)-(3.100) будем искать в виде разложения в ряд по собственным функциям (3.96) и (3.97): где Im - модифицированные функции Бесселя 1 -го рода. Из задачи (3.95), (3.98) - (3.100), (3.112) следует, что отклонение Выше уже отмечалось, что в главном порядке V0 содержит только касательные к твердой поверхности компоненты V0 = U0er + V0ea. Исходя из условия (3.103) и вида потенциала скорости (3.112), решение задачи (3.101) — (3.104) будет выглядеть следующим образом при z = ±1/2: Ї" 7/1=0 п=0 Из условия непрерывности (3.102) находим вертикальную компоненту W, скорости первого порядка